PCA in practice.
Principal Component Analysis(PCA) is a very important skill for dimention reduction to analyze high-dimentional data. High-dimentional data are data with features (p) a lot more than observations (n). This types of data are very commonly generated from high-throuput sequencing experiments. For example, an RNA-seq or microarry experiment measures expression of tens of thousands of genes for only 8 samples (4 controls and 4 treatments).
Let’s use a microarray data for demonstration. One thing to note is that in linear algebra, a matrix is coded as n (rows are observations) X p (columns are features).However, in the microarray/RNA-seq case, the matrix is represented as p (rows are features/genes) X n (columns are observations/samples). That’s why we need to transpose the matrix before feeding the matrix to prcomp or SVD.
library(ISLR)
# transpose the data
ncidat<- t(NCI60$data)
colnames(ncidat)<- NCI60$labs
dim(ncidat)## [1] 6830 64## it is a data matrix with 64 columns (different tissues) and 6830 rows (genes)
ncidat[1:6,1:6]## CNS CNS CNS RENAL BREAST CNS
## 1 0.300 0.679961 0.940 2.800000e-01 0.485 0.310
## 2 1.180 1.289961 -0.040 -3.100000e-01 -0.465 -0.030
## 3 0.550 0.169961 -0.170 6.800000e-01 0.395 -0.100
## 4 1.140 0.379961 -0.040 -8.100000e-01 0.905 -0.460
## 5 -0.265 0.464961 -0.605 6.250000e-01 0.200 -0.205
## 6 -0.070 0.579961 0.000 -1.387779e-17 -0.005 -0.540Use prcomp
The default R package stats comes with function prcomp() to perform principal component analysis. This means that we don’t need to install anything (although there are other options using external packages).
We take the transpose of ncidat because prcomp assumes: units/samples in row and features (genes) in columns.
## please look at the help page to see the meanings of center and scale. parameters.
## center and scale can affect the result a lot. Usually we center the data.
pca_prcomp<- prcomp(t(ncidat), center = TRUE, scale. = FALSE)How much variantion is explained by each component:
plot(pca_prcomp)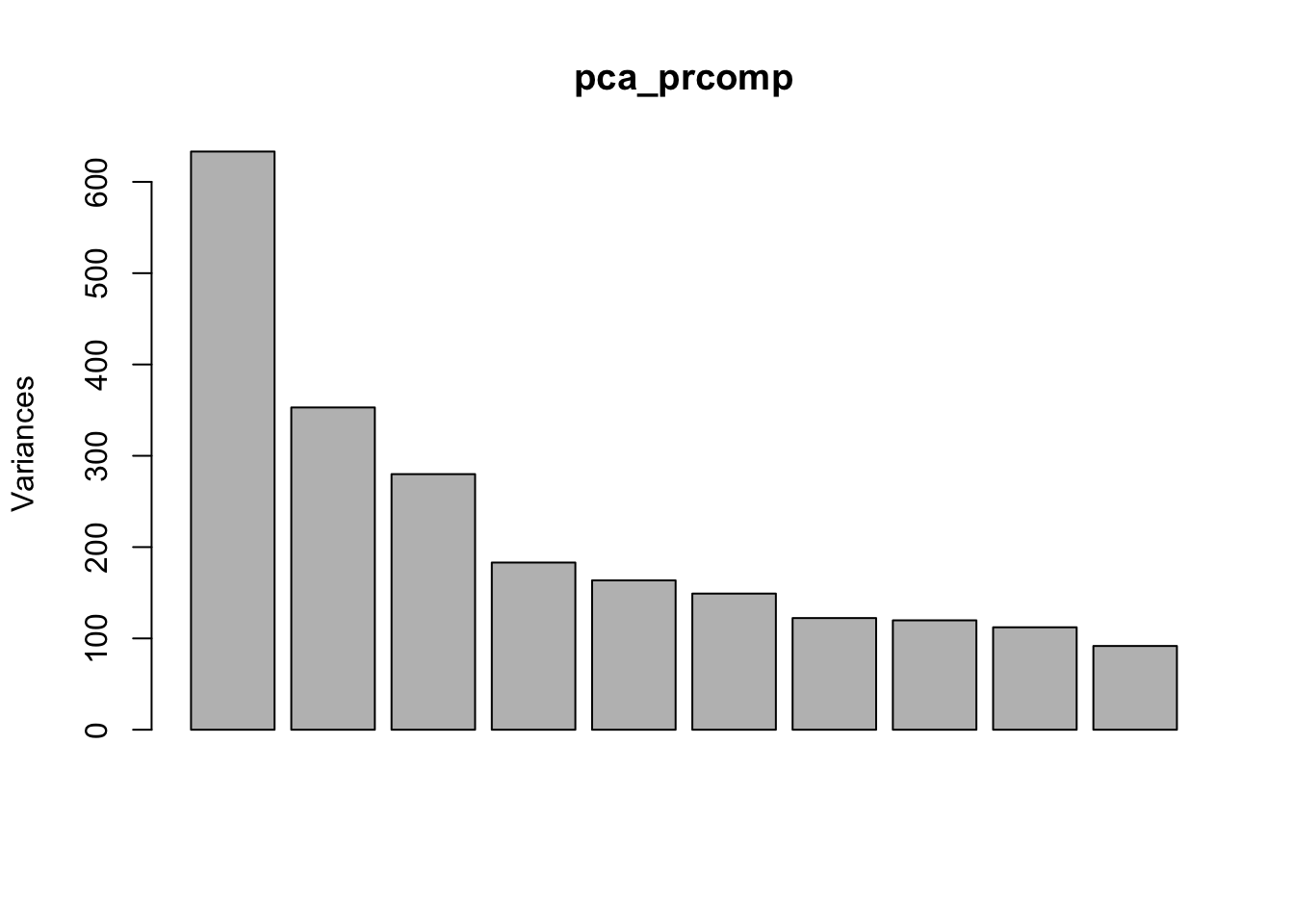
summary(pca_prcomp)## Importance of components:
## PC1 PC2 PC3 PC4 PC5
## Standard deviation 25.1638 18.78637 16.73078 13.53082 12.78895
## Proportion of Variance 0.1489 0.08301 0.06584 0.04306 0.03847
## Cumulative Proportion 0.1489 0.23194 0.29777 0.34083 0.37930
## PC6 PC7 PC8 PC9 PC10 PC11
## Standard deviation 12.21052 11.05840 10.94492 10.59140 9.57657 9.4493
## Proportion of Variance 0.03507 0.02876 0.02817 0.02638 0.02157 0.0210
## Cumulative Proportion 0.41437 0.44313 0.47130 0.49769 0.51926 0.5403
## PC12 PC13 PC14 PC15 PC16 PC17
## Standard deviation 9.22659 8.8220 8.66863 8.43185 8.2746 8.19031
## Proportion of Variance 0.02002 0.0183 0.01767 0.01672 0.0161 0.01578
## Cumulative Proportion 0.56028 0.5786 0.59626 0.61298 0.6291 0.64486
## PC18 PC19 PC20 PC21 PC22 PC23
## Standard deviation 7.86272 7.84561 7.74753 7.64167 7.41462 7.3207
## Proportion of Variance 0.01454 0.01448 0.01412 0.01373 0.01293 0.0126
## Cumulative Proportion 0.65940 0.67388 0.68799 0.70173 0.71466 0.7273
## PC24 PC25 PC26 PC27 PC28 PC29
## Standard deviation 7.09512 7.0817 6.86791 6.71857 6.6190 6.57295
## Proportion of Variance 0.01184 0.0118 0.01109 0.01062 0.0103 0.01016
## Cumulative Proportion 0.73910 0.7509 0.76199 0.77261 0.7829 0.79307
## PC30 PC31 PC32 PC33 PC34 PC35
## Standard deviation 6.50142 6.38411 6.31688 6.10274 6.07004 5.96433
## Proportion of Variance 0.00994 0.00959 0.00938 0.00876 0.00867 0.00837
## Cumulative Proportion 0.80302 0.81260 0.82199 0.83075 0.83941 0.84778
## PC36 PC37 PC38 PC39 PC40 PC41
## Standard deviation 5.93322 5.87286 5.82866 5.67923 5.63268 5.5707
## Proportion of Variance 0.00828 0.00811 0.00799 0.00759 0.00746 0.0073
## Cumulative Proportion 0.85606 0.86417 0.87216 0.87975 0.88721 0.8945
## PC42 PC43 PC44 PC45 PC46 PC47
## Standard deviation 5.51265 5.4555 5.37942 5.32142 5.1743 5.14470
## Proportion of Variance 0.00715 0.0070 0.00681 0.00666 0.0063 0.00623
## Cumulative Proportion 0.90165 0.9086 0.91546 0.92212 0.9284 0.93464
## PC48 PC49 PC50 PC51 PC52 PC53
## Standard deviation 5.01790 4.82436 4.77879 4.69168 4.5637 4.49039
## Proportion of Variance 0.00592 0.00547 0.00537 0.00518 0.0049 0.00474
## Cumulative Proportion 0.94057 0.94604 0.95141 0.95659 0.9615 0.96623
## PC54 PC55 PC56 PC57 PC58 PC59
## Standard deviation 4.41142 4.2741 4.21355 4.08613 3.91956 3.78810
## Proportion of Variance 0.00458 0.0043 0.00418 0.00393 0.00361 0.00337
## Cumulative Proportion 0.97081 0.9751 0.97928 0.98320 0.98682 0.99019
## PC60 PC61 PC62 PC63 PC64
## Standard deviation 3.52405 3.22882 3.15278 2.9856 1.341e-14
## Proportion of Variance 0.00292 0.00245 0.00234 0.0021 0.000e+00
## Cumulative Proportion 0.99311 0.99557 0.99790 1.0000 1.000e+00#sdev refers to the standard deviation of principal components.
pca_prcomp$sdev## [1] 2.516378e+01 1.878637e+01 1.673078e+01 1.353082e+01 1.278895e+01
## [6] 1.221052e+01 1.105840e+01 1.094492e+01 1.059140e+01 9.576574e+00
## [11] 9.449313e+00 9.226590e+00 8.821954e+00 8.668634e+00 8.431849e+00
## [16] 8.274578e+00 8.190308e+00 7.862721e+00 7.845612e+00 7.747529e+00
## [21] 7.641665e+00 7.414624e+00 7.320674e+00 7.095120e+00 7.081674e+00
## [26] 6.867907e+00 6.718573e+00 6.618968e+00 6.572955e+00 6.501420e+00
## [31] 6.384107e+00 6.316878e+00 6.102743e+00 6.070035e+00 5.964333e+00
## [36] 5.933221e+00 5.872856e+00 5.828663e+00 5.679232e+00 5.632684e+00
## [41] 5.570718e+00 5.512649e+00 5.455510e+00 5.379416e+00 5.321422e+00
## [46] 5.174272e+00 5.144699e+00 5.017899e+00 4.824356e+00 4.778789e+00
## [51] 4.691679e+00 4.563740e+00 4.490394e+00 4.411423e+00 4.274070e+00
## [56] 4.213548e+00 4.086132e+00 3.919560e+00 3.788098e+00 3.524054e+00
## [61] 3.228818e+00 3.152782e+00 2.985601e+00 1.341106e-14## variance explained by each PC cumulatively
cumsum(pca_prcomp$sdev^2)/sum(pca_prcomp$sdev^2)## [1] 0.1489294 0.2319364 0.2977720 0.3408323 0.3793002 0.4143671 0.4431287
## [8] 0.4713030 0.4976867 0.5192567 0.5402571 0.5602793 0.5785838 0.5962576
## [15] 0.6129791 0.6290826 0.6448598 0.6594001 0.6738773 0.6879947 0.7017289
## [22] 0.7146592 0.7272638 0.7391037 0.7508988 0.7619925 0.7726091 0.7829132
## [29] 0.7930745 0.8030158 0.8126016 0.8219866 0.8307461 0.8394120 0.8477786
## [36] 0.8560582 0.8641702 0.8721606 0.8797465 0.8872086 0.8945074 0.9016548
## [43] 0.9086548 0.9154609 0.9221211 0.9284180 0.9346431 0.9405652 0.9460392
## [50] 0.9514103 0.9565874 0.9614860 0.9662284 0.9708055 0.9751019 0.9792776
## [57] 0.9832045 0.9868178 0.9901928 0.9931137 0.9955657 0.9979035 1.0000000
## [64] 1.0000000what’s in the prca_prcomp object
names(pca_prcomp)## [1] "sdev" "rotation" "center" "scale" "x"## the first two PCs for the first 6 tissues
head(pca_prcomp$x[,1:2])## PC1 PC2
## CNS -19.79578 0.1152691
## CNS -21.54610 -1.4573503
## CNS -25.05662 1.5260929
## RENAL -37.40954 -11.3894784
## BREAST -50.21864 -1.3461737
## CNS -26.43520 0.4629819PC1_and_PC2<- data.frame(PC1=pca_prcomp$x[,1], PC2= pca_prcomp$x[,2], type = rownames(pca_prcomp$x))
## plot PCA plot
library(ggplot2)## Warning: package 'ggplot2' was built under R version 3.5.2ggplot(PC1_and_PC2, aes(x=PC1, y=PC2, col=type)) + geom_point() + geom_text(aes(label = type), hjust=0, vjust=0)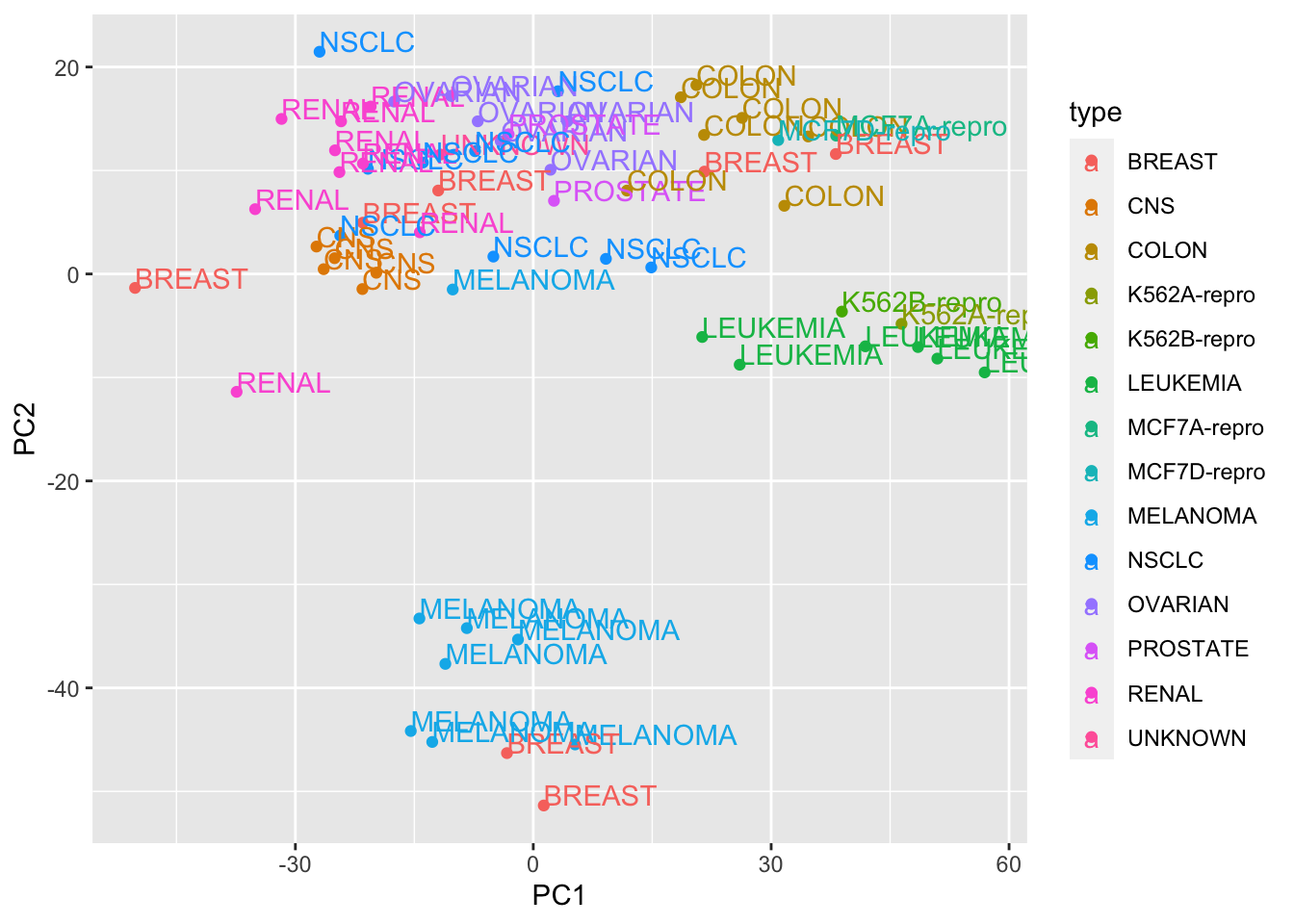
#This returns each principal components loadings
pca_prcomp$rotation[1:6, 1:6]## PC1 PC2 PC3 PC4 PC5
## 1 -0.005096247 0.0009839929 0.002116058 0.007628801 -0.012118316
## 2 -0.001642354 0.0034355664 0.008049350 0.004910196 -0.007412249
## 3 -0.002509243 -0.0015838271 0.004746350 0.008769557 -0.012426296
## 4 0.004940063 0.0078435347 0.013716214 0.011378816 -0.014851587
## 5 -0.003365039 -0.0002680479 0.010677453 -0.005249648 -0.003317312
## 6 0.001382038 -0.0034431320 0.003167842 0.007425971 -0.002879251
## PC6
## 1 0.0061392242
## 2 0.0114429879
## 3 -0.0002860562
## 4 -0.0065009935
## 5 -0.0003513787
## 6 0.0003210365Use singluar value decomposition
in a svd analysis, a matrix n x p matrix X is decomposed by X = U*D*V:
1.U is an m×n orthogonal matrix.
2.V is an n×n orthogonal matrix.
3.D is an n×n diagonal matrix.
PCs: Z = XV or Z = UD (U are un-scaled PCs)
Some facts of PCA:
k th column of Z, Z(k), is the k th PC.(the k th pattern)
PC loadings: V k th column of V, V(k) is the k th PC loading (feature weights). aka. the k th column of V encodes the associated k th pattern in feature space.
PC loadings: U k th column of U, U(k) is the k th PC loading (observation weights). aka. the k th column of U encodes the associated k th pattern in observation space.
Diagnal matrix: D diagnals in D: d(k) gives the strength of the k th pattern.
Variance explained by k th PC: d(k)^2 Total variance of the data: sum(d(k1)^2 + d(k2)^2 + …..d(k)^2+….)
proportion of variane explained by k th PC: d(k)^2 / sum(d(k1)^2 + d(k2)^2 + …..d(k)^2+….)
X<- t(scale(t(ncidat),center=TRUE,scale=FALSE))
# we transpose X again for svd
# usually there is no need to transpose the matrix and then transpose it back, but svd was written that rows are observations and columns are
# features.however, most genomic data represent observations (e.g. samples) in columns and features (e.g. genes) in columns.
sv<- svd(t(X))
U<- sv$u
V<- sv$v
D<- sv$d
## U are un-scaled PC, Z is scaled
Z<- t(X)%*%V
## PCs
Z[1:6, 1:6]## [,1] [,2] [,3] [,4] [,5] [,6]
## CNS -19.79578 0.1152691 -5.968917 4.753293 -4.882164 18.92591
## CNS -21.54610 -1.4573503 -9.019584 6.767942 -2.247604 17.07273
## CNS -25.05662 1.5260929 -6.959653 2.785913 -10.819648 16.45389
## RENAL -37.40954 -11.3894784 -5.407097 15.442094 -16.011475 33.09651
## BREAST -50.21864 -1.3461737 -17.599944 15.099862 -13.852847 16.94340
## CNS -26.43520 0.4629819 -16.931456 11.389195 -6.742920 11.85838## is the same as
pca_prcomp$x[1:6, 1:6]## PC1 PC2 PC3 PC4 PC5 PC6
## CNS -19.79578 0.1152691 -5.968917 4.753293 -4.882164 18.92591
## CNS -21.54610 -1.4573503 -9.019584 6.767942 -2.247604 17.07273
## CNS -25.05662 1.5260929 -6.959653 2.785913 -10.819648 16.45389
## RENAL -37.40954 -11.3894784 -5.407097 15.442094 -16.011475 33.09651
## BREAST -50.21864 -1.3461737 -17.599944 15.099862 -13.852847 16.94340
## CNS -26.43520 0.4629819 -16.931456 11.389195 -6.742920 11.85838## PC loadings
V[1:6, 1:6]## [,1] [,2] [,3] [,4] [,5]
## [1,] -0.005096247 0.0009839929 0.002116058 0.007628801 -0.012118316
## [2,] -0.001642354 0.0034355664 0.008049350 0.004910196 -0.007412249
## [3,] -0.002509243 -0.0015838271 0.004746350 0.008769557 -0.012426296
## [4,] 0.004940063 0.0078435347 0.013716214 0.011378816 -0.014851587
## [5,] -0.003365039 -0.0002680479 0.010677453 -0.005249648 -0.003317312
## [6,] 0.001382038 -0.0034431320 0.003167842 0.007425971 -0.002879251
## [,6]
## [1,] 0.0061392242
## [2,] 0.0114429879
## [3,] -0.0002860562
## [4,] -0.0065009935
## [5,] -0.0003513787
## [6,] 0.0003210365## is the same as
pca_prcomp$rotation[1:6, 1:6]## PC1 PC2 PC3 PC4 PC5
## 1 -0.005096247 0.0009839929 0.002116058 0.007628801 -0.012118316
## 2 -0.001642354 0.0034355664 0.008049350 0.004910196 -0.007412249
## 3 -0.002509243 -0.0015838271 0.004746350 0.008769557 -0.012426296
## 4 0.004940063 0.0078435347 0.013716214 0.011378816 -0.014851587
## 5 -0.003365039 -0.0002680479 0.010677453 -0.005249648 -0.003317312
## 6 0.001382038 -0.0034431320 0.003167842 0.007425971 -0.002879251
## PC6
## 1 0.0061392242
## 2 0.0114429879
## 3 -0.0002860562
## 4 -0.0065009935
## 5 -0.0003513787
## 6 0.0003210365# plot PC1 vs PC2
pc_dat<- data.frame(type = rownames(Z), PC1 = Z[,1], PC2= Z[,2])
ggplot(pc_dat,aes(x=PC1, y=PC2, col=type)) + geom_point() + geom_text(aes(label = type), hjust=0, vjust=0)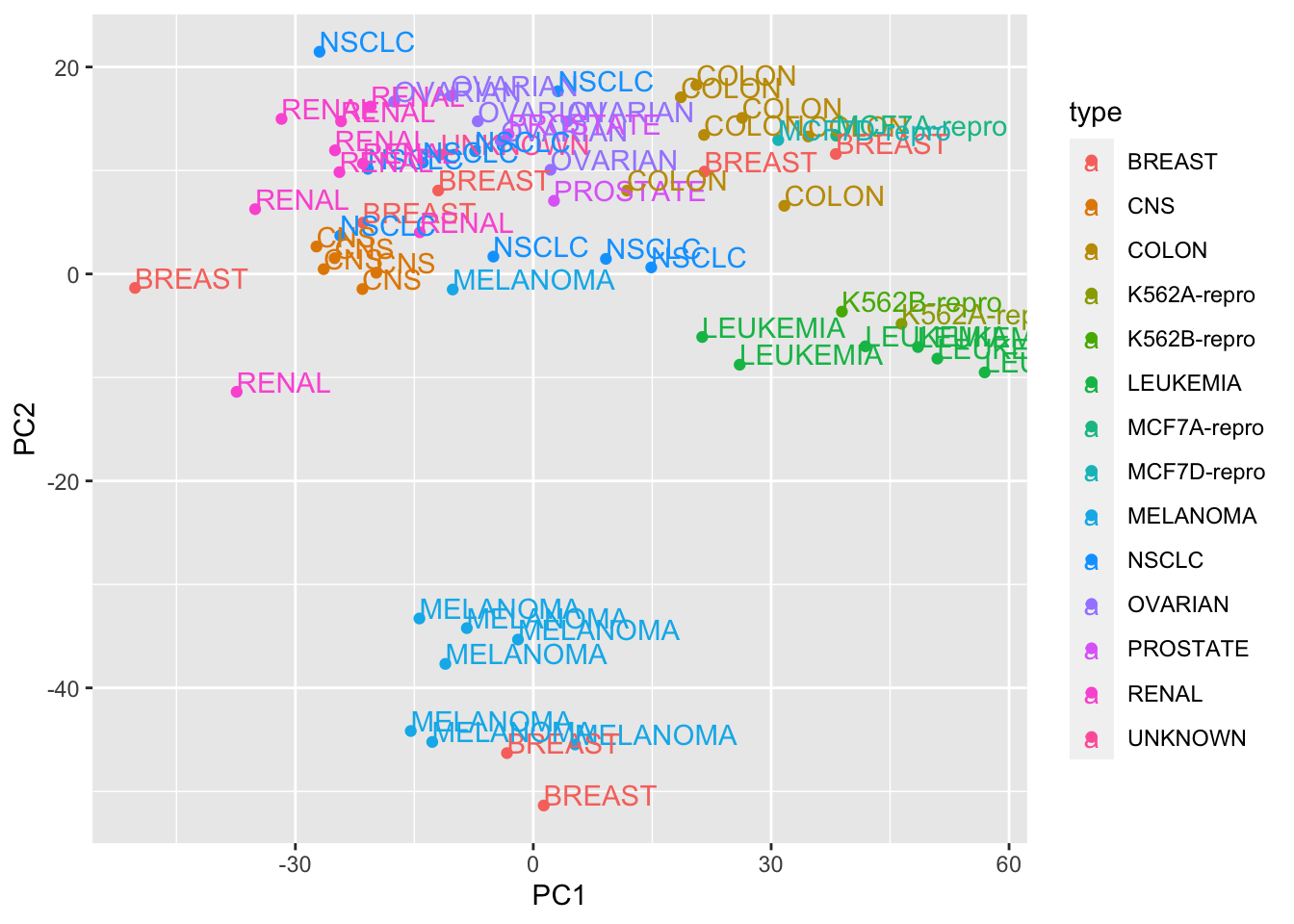
We get the same results as from the prcomp function.
Variance explained for each PC
varex = 0
cumvar = 0
denom = sum(D^2)
for(i in 1:length(D)){
varex[i] = D[i]^2/denom
cumvar[i] = sum(D[1:i]^2)/denom
}
## variance explained by each PC cumulatively
cumvar## [1] 0.1489294 0.2319364 0.2977720 0.3408323 0.3793002 0.4143671 0.4431287
## [8] 0.4713030 0.4976867 0.5192567 0.5402571 0.5602793 0.5785838 0.5962576
## [15] 0.6129791 0.6290826 0.6448598 0.6594001 0.6738773 0.6879947 0.7017289
## [22] 0.7146592 0.7272638 0.7391037 0.7508988 0.7619925 0.7726091 0.7829132
## [29] 0.7930745 0.8030158 0.8126016 0.8219866 0.8307461 0.8394120 0.8477786
## [36] 0.8560582 0.8641702 0.8721606 0.8797465 0.8872086 0.8945074 0.9016548
## [43] 0.9086548 0.9154609 0.9221211 0.9284180 0.9346431 0.9405652 0.9460392
## [50] 0.9514103 0.9565874 0.9614860 0.9662284 0.9708055 0.9751019 0.9792776
## [57] 0.9832045 0.9868178 0.9901928 0.9931137 0.9955657 0.9979035 1.0000000
## [64] 1.0000000It is the same as the result of cumsum(pca_prcomp$sdev^2)/sum(pca_prcomp$sdev^2) above.
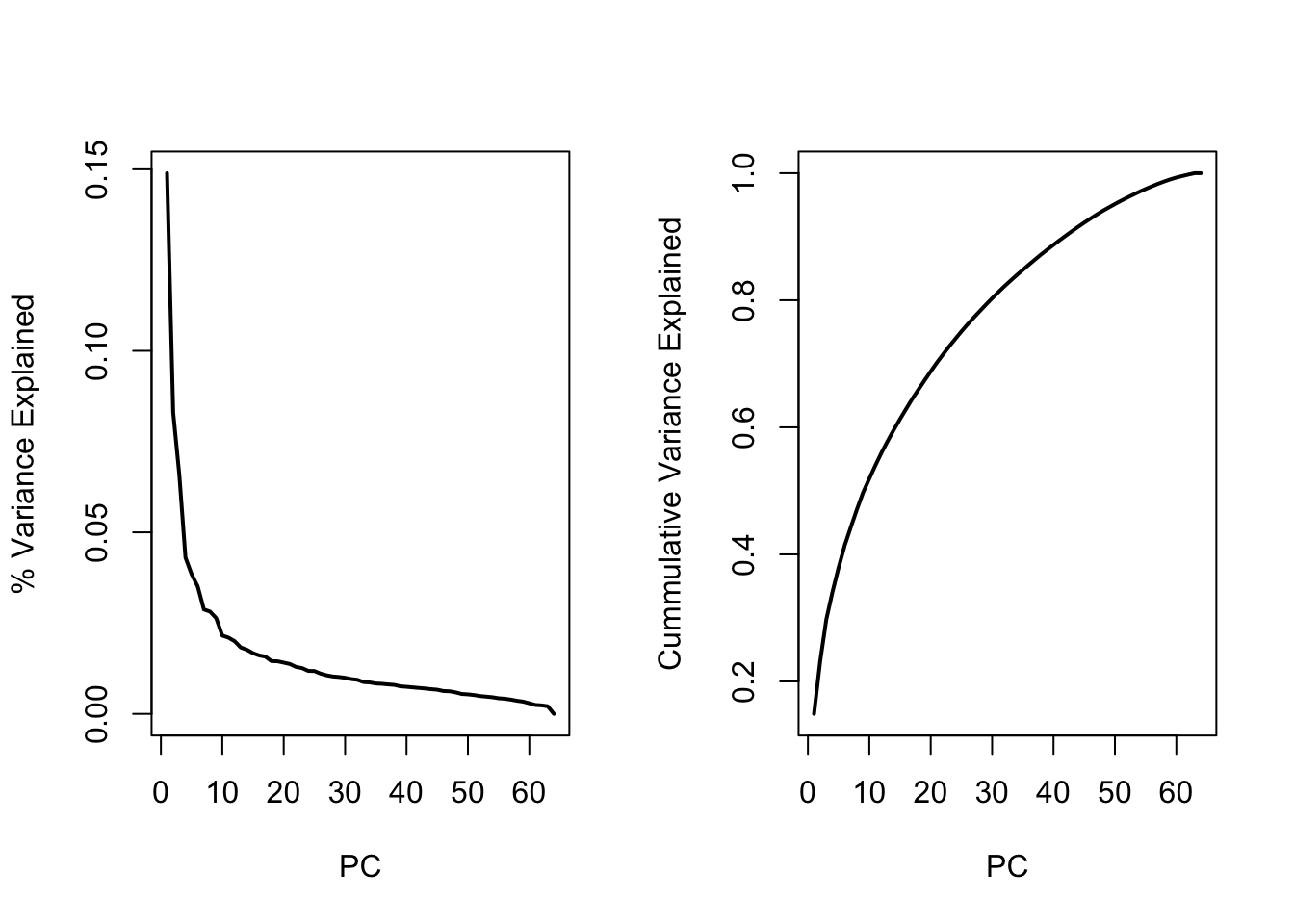
Screeplot
par(mfrow=c(1,2))
plot(1:length(D),varex,type="l",lwd=2,xlab="PC",ylab="% Variance Explained")
plot(1:length(D),cumvar,type="l",lwd=2,xlab="PC",ylab="Cummulative Variance Explained")